Umschlaeng Proportiment: Ein umfassender Leitfaden

Proportionalität ist ein grundlegend wichtiger Aspekt in der Mathematik, der in vielen Bereichen Anwendung findet, von der Alltagssituation bis zur Wissenschaft. In diesem Artikel beschäftigen wir uns mit der Idee der Umschlaeng Proportiment, insbesondere mit direkter und inverser Proportionalität. Wussten Sie, dass viele Alltagsphänomene wie Geschwindigkeit und Zeitverhältnisse durch Proportionalität beschrieben werden können? In diesem Artikel erfahren Sie, wie Proportionalität funktioniert, welche Arten es gibt und wie Sie diese Konzepte in der Praxis anwenden können. Besuchen Sie auch die erste Ressource und die zweite Ressource, um mehr über verwandte Themen zu erfahren.

Einführung in die Proportionalität

Proportionalität beschreibt eine Beziehung zwischen zwei Größen. Wenn sich eine Größe ändert, ändert sich eine andere Größte in einem festen Verhältnis. Es gibt zwei Hauptarten der Proportionalität: die direkte Proportionalität und die inverse Proportionalität.

Was ist direkte Proportionalität?

Bei der direkten Proportionalität sind zwei Größen direkt proportional zueinander, wenn eine Verdopplung der einen Größe auch die Verdopplung der anderen zur Folge hat. Ein einfaches Beispiel wäre die Beziehung zwischen der Anzahl der gekauften Äpfel und dem Gesamtpreis, den Sie bezahlen müssen.

• Wenn Sie 1 Apfel für 1 Euro kaufen, dann kosten 2 Äpfel 2 Euro.
• Mathematisch ausgedrückt: y = k * x, wobei k eine Konstante ist.

Was ist inverse Proportionalität?

Die inverse Proportionalität beschreibt eine Beziehung, bei der eine Größe zunimmt, wenn die andere abnimmt. Ein typisches Beispiel dafür ist die Anzahl der Arbeiter, die an einem Projekt beteiligt sind. Je mehr Arbeiter Sie haben, desto weniger Zeit benötigen sie, um die Aufgabe zu beenden.

• Wenn 4 Arbeiter 10 Stunden benötigen, dann benötigen 2 Arbeiter 20 Stunden.
• Mathematisch: y = k / x, wobei k eine Konstante ist.

Graphische Darstellung von Proportionalität

Um die Konzepte der direkten und inversen Proportionalität besser zu verstehen, ist es hilfreich, sie grafisch darzustellen. Im folgenden Bild wird die direkte und inverse Proportionalität veranschaulicht:

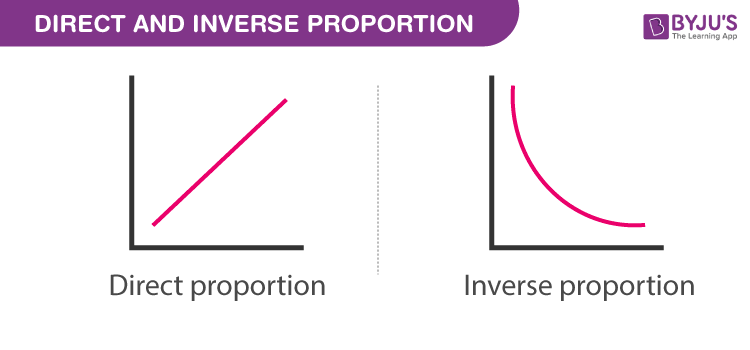
Grafik der direkten Proportionalität

In der Grafik sehen wir eine gerade Linie, die durch den Ursprung verläuft. Dies zeigt, dass, wenn eine Größe steigt, die andere ebenfalls proportional steigt.

Grafik der inversen Proportionalität

Die Grafik der inversen Proportionalität zeigt eine Kurve, die von oben nach unten verläuft. Dieses Muster zeigt, dass, wenn eine Größe steigt, die andere abnimmt.

Praktische Anwendungen der Proportionalität

Proportionalität findet in vielen Bereichen der Wissenschaft und des täglichen Lebens Anwendung. Hier sind einige Beispiele:

1. Wissenschaftliche Experimente

In der Physik wird oft die Beziehung zwischen Geschwindigkeit, Zeit und Distanz betrachtet. Diese Größen sind direkt proportional:

• Wenn Sie schneller fahren, benötigen Sie weniger Zeit, um eine bestimmte Strecke zurückzulegen.

2. Wirtschaft

In der Finanzwelt ist das Verhältnis zwischen Angebot und Nachfrage oft invers proportional. Wenn das Angebot an einem Produkt steigt, sinkt in der Regel der Preis:

• Hohe Nachfrage und geringes Angebot führen oft zu höheren Preisen.

3. Alltag

Im Alltag können Sie Proportionalität in vielen Situationen beobachten, sei es beim Kochen, beim Einkaufen oder beim Zeitmanagement:

• Wenn Sie mehr Zutaten haben, erhöhen sich die Portionen entsprechend.

Verständnis und Übungen zur Proportionalität

Um sicherzustellen, dass Sie die Konzepte der Proportionalität gut verstehen, hier einige Übungen:

Übung: Direkte Proportionalität

Wenn 3 Äpfel 1,50 Euro kosten, wie viel kosten 6 Äpfel?

Übung: Inverse Proportionalität

Wenn 5 Arbeiter 15 Stunden für ein Projekt benötigen, wie viele Stunden benötigen 10 Arbeiter für dasselbe Projekt?

Zusammenfassung und Schlussfolgerung

Die Konzepte der direkten und inversen Proportionalität sind fundamentale Bestandteile der Mathematik, die Ihnen helfen, die Welt um Sie herum besser zu verstehen. Ob in der Wissenschaft, Wirtschaft oder im Alltag, diese Beziehungen sind allgegenwärtig. Durch das Verständnis dieser Konzepte können Sie präziser in Ihren Berechnungen und Analysen sein.

Wir hoffen, dass dieser Artikel Ihnen wertvolle Einblicke und praktisches Wissen zu den Themen Umschlaeng Proportiment, direkte und inverse Proportionalität vermittelt hat. Für weitere Informationen und Übungen empfehlen wir Ihnen die oben angegebenen Links, um Ihr Wissen zu vertiefen.